优化-4-近接勾配法

近接勾配法 Proximal Gradient Method

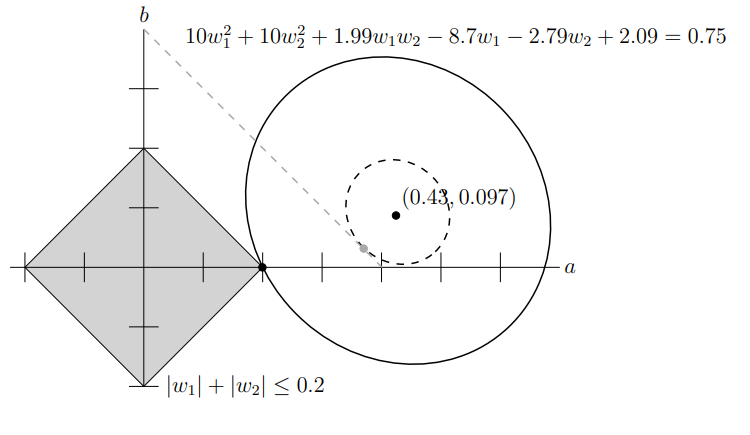
有时候我们的求解的优化问题带有约束，例如当我们希望结果稀疏化时，可以使用 LASSO 来约束目标，即

$$||x||_1\leq \lambda$$

形式化的说，考虑凸包 与凸函数 ，我们有优化目标

$$\min_{x} f(x)\quad s.t.\quad x\in X$$

此时可以使用近接勾配法 Proximal Gradient Method 进行求解。

Projected Gradient Descent

Algorithm

求解带凸包约束的凸优化问题，一个直观的想法就是每一步迭代就如梯度下降法一样进行，但是在更新 时，我们需要将其投影到凸包 中。这样的方法称为 Projected Gradient Descent，如下图所示。

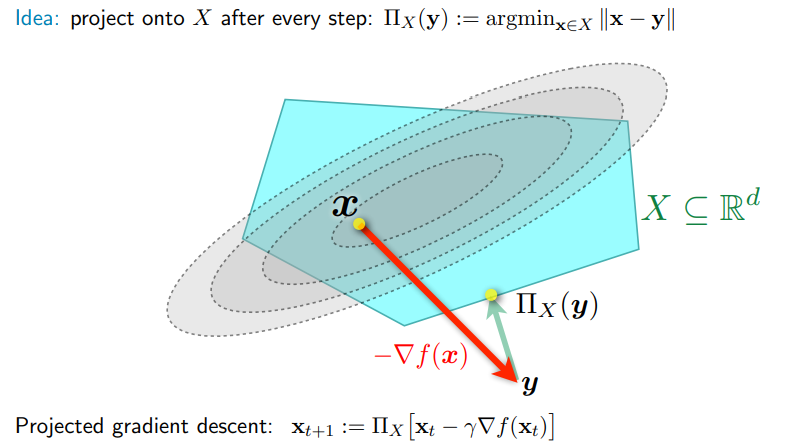
算法流程如下：

• INPUT: 优化目标 , 凸包约束 , 步长
• S1: 随机初始化解
• S2: 计算梯度
• S3: 梯度下降
• S4: 计算投影
• S5：回到 S2 直到算法收敛
• OUTPUT:

Convergence

事实上，Projected Gradient Descent 算法收敛率和朴素的梯度下降法一致，即

• Lischitz Convex Function:
• Smooth Convex Function:
• Smooth and Strongly Convex Function:

以下给出证明：

我们首先给出两个关于投影的性质，对闭集凸包 ， 凸包内一点 ，任意点 ，满足

利用几何性质容易证明上述结论，这里不再赘述。

Vanilla Analysis

不失一般性，这里首先给出 Vanilla Analysis 收敛性的证明。

将 替换为 ，由梯度下降步的定义 有

$$\langle g_t,x_t-x^* \rangle = \frac{1}{\gamma}\langle x_t-\underline{y_{t+1}},x_t-x^*\rangle$$

利用 改写右项，有

$$\langle g_t,x_t-x^* \rangle = \frac{\gamma}{2} ||g_t||^2 + \frac{1}{2\gamma} \left(||x_t-x^*||^2-||\underline{y_{t+1}}-x^*||^2 \right)$$

利用投影性质 2，由 ，有

$$\begin{aligned} ||x^*-y_{t+1}||^2 & \geq ||x^*-\Pi_X(y_{t+1})||^2 + ||y_{t+1}-\Pi_X(y_{t+1})||^2 \\ & \geq ||x^*-\Pi_X(y_{t+1})||^2 \\ & \geq ||x^*-x_{t+1}||^2 \end{aligned}$$

代回，有

$$\langle g_t,x_t-x^* \rangle \leq \frac{\gamma}{2} ||g_t||^2 + \frac{1}{2\gamma} \left(||x_t-x^*||^2-||x_{t+1}-x^*||^2 \right)$$

利用凸函数性质，求和得到平均误差上界

$$\sum_{t=0}^{T-1}\left( f(x_t)-f(x^*) \right) \leq \frac{\gamma}{2} \sum_{t=0}^{T-1}||g_t||^2 + \frac{1}{2\gamma} ||x_0-x^*||^2$$

接下来利用投影的两个性质容易证明几种 assumption 下的收敛性，此处不再赘述。

然而，在实际计算时，计算投影同样被视为对 Oracle 的一次查询，可能会非常耗时。仍考虑 LASSO 的 L1 norm 限制，在 维情形下，需要计算到 个面的距离，非常耗时。如果是 L2 norm 限制，计算量几乎可以忽略不计。

Proximal Gradient Descent

Composite Optimization Problems

考虑目标函数

$$f(x):=g(x) + h(x)$$

其中 是满足各种用于证明收敛率假设的凸函数， 是一个任意的不满足上述性质函数。这个问题比上一节中介绍的带约束的优化问题更一般，因为如果 是一个指示函数

$$h(x) = \mathbb{I}[x\in X]=\begin{cases} 0, & x\in X \\ \infty, & x\notin X \end{cases}$$

其中 是一个凸的闭集，那么 就等价于一个带约束的优化问题。

现在考虑如何优化。如果只考虑性质良好的 ，可以使用经典的梯度下降算法最小化二次上界

$$x_{t+1} = \arg\min_y g(x_t) + \langle \nabla g(x_t), y-x_t \rangle + \frac{L}{2}||y-x_t||^2$$

现在对于 ，加入 ，有

$$\begin{aligned} x_{t+1} & = \arg\min_y g(x_t) + \langle \nabla g(x_t), y-x_t \rangle + \frac{L}{2}||y-x_t||^2 + h(y) \\ & = \arg\min_y \langle \nabla g(x_t), y \rangle + \frac{L}{2}||y-x_t||^2 + h(y) \\ & = \arg\min_y \frac{L}{2}||y||^2 - L\langle x_t-\frac{1}{L}\nabla g(x_t), y \rangle + h(y) \\ & = \arg\min_y \frac{L}{2} \left(||y||^2- 2\langle x_t-\frac{1}{L}\nabla g(x_t), y \rangle\right) + h(y) \\ & = \arg\min_y \frac{L}{2} ||y - (x_t-\frac{1}{L}\nabla g(x_t))||^2 + h(y) \\ \end{aligned}$$

则得到了 Proximal Gradient Descent 的更新公式，即

$$x_{t+1}:=\textbf{prox}_{h,\frac{1}{L}}(x_t-\frac{1}{L}\nabla g(x_t))$$

其中

$$\textbf{prox}_{h,\frac{1}{L}}(z) := \arg\min_y \frac{L}{2}||y-z||^2 + h(y)$$

当 时，算法退化为普通的梯度下降法；当 , 算法退化为 Projected Gradient Descent; 因此可以声称 Proximal Gradient Descent 是梯度下降算法的一般化。

Convergence

收敛性可以参考 Yurri Nesterov。

收敛性证明和普通情形下相似，唯一需要注意的是新加入的 ，我们有如下定理。

考虑凸函数 且 同时满足 L Smooth ，令 ，如果

$$f(x_0)-f(x^*)\leq R_0^2=L\max_{x\in f^{\leq f(x_0)}}||x-x^*||^2$$

则有

$$f(x_t)-f(x^*)\leq\frac{2R_0^2}{t}$$

以下给出证明。由 Proximal Gradient Descent 的更新公式，有

$$f(x_{t+1}) \leq min_y \left( g(y) + \langle \nabla g(x_t), y-x_t \rangle + \frac{L}{2}||x_t-y||^2 + h(y) \right)$$

由凸性，有

$$g(x_t) + \langle \nabla g(x_t), y-x_t \rangle \leq g(y)$$

代入上式，有

$$\begin{aligned} f(x_{t+1}) & \leq min_y \left( g(y) + \frac{L}{2}||x_t-y||^2 + h(y) \right) \\ & = min_y \left( f(y) + \frac{L}{2}||x_t-y||^2 \right) \end{aligned}$$

原先 ，现在将 限制在 到 的连线上，解空间变小，从而最小值变大。令 ，有

$$\begin{aligned} f(x_{t+1}) & \leq min_{\alpha\in[0,1]} \left( f(\alpha x^*+(1-\alpha)x_t) + \frac{L}{2}||\alpha x^*+(1-\alpha)x_t-x_t||^2 \right) \\ & = min_{\alpha\in[0,1]} \left( f(\alpha x^*+(1-\alpha)x_t) + \frac{L\alpha^2}{2}|| x^*- x_t||^2 \right) \\ \end{aligned}$$

由 凸性，有

$$f(\alpha x^*+(1-\alpha)x_t) \leq \alpha f(x^*) + (1-\alpha)f(x_t)$$

代入上式，有

$$\begin{aligned} f(x_{t+1}) & \leq min_{\alpha\in[0,1]} \left( \alpha f(x^*) + (1-\alpha)f(x_t) + \frac{L\alpha^2}{2}|| x^*- x_t||^2 \right) \\ & = min_{\alpha\in[0,1]} \left( f(x_t) - \alpha(f(x_t)-f(x^*)) + \frac{L\alpha^2}{2}|| x^*- x_t||^2 \right) \\ & \leq min_{\alpha\in[0,1]} \left( f(x_t) - \alpha(f(x_t)-f(x^*)) + \alpha^2\frac{LR_0^2}{2} \right) \\ \end{aligned}$$

由于 内部是关于 的二次函数，容易得到其中当前单步最优解 为

$$\alpha^* = \min\left\{ \frac{f(x_t)-f(x^*)}{L R_0^2}, 1 \right\}$$

继续讨论收敛性，分类讨论之：

• 当 时，有 ，代入上文最小化目标，有

  $$f(x_{t+1})\le f(x^*) + \frac{L R_0^2}{2}$$

  于是有

  $$f(x_{t+1}) - f(x^*)\leq \frac{L R_0^2}{2} < \frac{1}{2}(f(x_t)-f(x^*))$$

  此情形下会指数级速度收敛。

• 当 ，代入，有

  $$f(x_{t+1})-f(x^*)\leq \left( 1-\frac{f(x_t)-f(x^*)}{2LR_0^2} \right) (f(x_t)-f(x^*))$$

  方便起见，记 ，有

  $$\xi_{t+1}\leq\left(1-\frac{\xi_t}{2LR_0^2}\right)\xi_t$$

  即

  $$\xi_{t+1}-\xi_{t}\leq \frac{\xi_t^2}{2LR_0^2}$$

  由于每一步迭代都是在最小化，且候选解包含原位置，因此 单调不增，于是有

  $$\frac{1}{\xi_{t+1}} - \frac{1}{\xi_t} = \frac{\xi_{t}-\xi_{t+1}}{\xi_{t+1}\xi_{t}} \geq \frac{\xi_{t}-\xi_{t+1}}{\xi_{t}^2} \geq \frac{1}{2LR_0^2}$$

  对前 项累加，有

  $$\frac{1}{\xi_t} \geq \frac{T}{2LR_0^2} + \frac{1}{\xi_0}$$

  因此有

  $$f(x_t)-f(x_*)\leq \frac{1}{\frac{T}{2LR_0^2}+\frac{1}{\xi_0}}\leq \frac{2LR_0^2}{T}$$

因此收敛性得证。