优化-3-梯度下降法

梯度下降法 Gradient Descent Method

本章中我们开始利用梯度信息解决最优化问题。基本的梯度下降法采用迭代法，基于“梯度方向是函数上升最快的方向”，每一轮迭代向梯度的反方向走一步，即

$$x_{t+1} := x_t - \gamma\nabla f(x_t)$$

其中 称为步长 stepsize，用于约束每一步走的长度。

Vanilla Analysis

为了方便进行收敛性分析，我们假定目标函数 是凸的，处处可导的，且有全局最优解 。

在实际计算时，我们往往难以找到精确解，因此对于优化目标

$$\min_x f(x)$$

我们往往目标会改为找到接近最优解的一个解即可，即

$$f(x) - f(x^*) \leq \epsilon$$

一个自然的问题是，我们如何约束 ？

方便起见，简写 表示 所在位置梯度。根据梯度下降的定义，我们有

$$\langle g_t,x_t-x^* \rangle = \frac{1}{\gamma}\langle x_t-x_{t+1},x_t-x^*\rangle$$

利用 改写右项，有

$$\begin{aligned} \langle g_t,x_t-x^* \rangle & = \frac{1}{2\gamma} \left(||x_t-x_{t+1}||^2+||x_t-x^*||^2-||x_{t+1}-x^*||^2 \right) \\ & = \frac{\gamma}{2} ||g_t||^2 + \frac{1}{2\gamma} \left(||x_t-x^*||^2-||x_{t+1}-x^*||^2 \right) \end{aligned}$$

将前 步累加，有

$$\sum_{t=0}^{T-1} \langle g_t,x_t-x^* \rangle = \frac{\gamma}{2} \sum_{t=0}^{T-1}||g_t||^2 + \frac{1}{2\gamma} \left(||x_0-x^*||^2-||x_{T}-x^*||^2 \right)$$

由凸函数性质，有

$$f(x_t)-f(x^*)\leq \langle g_t,x_t-x^* \rangle$$

将前 步累加，有

$$\sum_{t=0}^{T-1}\left( f(x_t)-f(x^*) \right) \leq \sum_{t=0}^{T-1} \langle g_t,x_t-x^* \rangle \leq \frac{\gamma}{2} \sum_{t=0}^{T-1}||g_t||^2 + \frac{1}{2\gamma} \left(||x_0-x^*||^2-||x_{T}-x^*||^2 \right)$$

于是可得关于平均误差的上界

$$\sum_{t=0}^{T-1}\left( f(x_t)-f(x^*) \right) \leq \frac{\gamma}{2} \sum_{t=0}^{T-1}||g_t||^2 + \frac{1}{2\gamma} ||x_0-x^*||^2$$

在这个简单的证明中，还存在几个问题

• 步长会对结果产生很大影响，不知道 等参数的情况下难以约束上界
• 不能保证最后一步就是最好的解

Lipschitz Convex Functions

要使上述上界可求，我们要对 增加额外的约束，一个简单的想法就是直接约束

$$\left\{ \begin{aligned} &\ ||\nabla f(x)||\leq B \\ &\ ||x_0-x^*||\leq R \end{aligned} \right.$$

其中对 的约束实质上就是 Lipschitz Continuity。

那么可以利用基本不等式得到 ，代回上一节所得平均误差上界可得

$$\sum_{t=0}^{T-1}\left( f(x_t)-f(x^*) \right) \leq RB\sqrt{T}$$

不妨设 $\hat{x}=\arg\min_{t=0}^T f(x_t)-f(x^*)$ 为 轮迭代中的最优解，则有

$$f(\hat{x})-f(x^*)\leq \frac{1}{T}\sum_{t=0}^{T-1}\left( f(x_t)-f(x^*) \right) \leq \frac{RB}{\sqrt{T}}$$

要使得误差降低到 以下，则有

$$f(\hat{x})-f(x^*) \leq \frac{RB}{\sqrt{T}} \leq \epsilon \Rightarrow T\geq \frac{R^2B^2}{\epsilon^2}$$

于是得到收敛率

$$T\sim \mathcal{O}(\frac{1}{\epsilon^2})$$

Smooth Convex Functions

Smoothness

对于处处可导的函数 ，如果满足

$$f(y)\leq f(x)+\langle\nabla f(x),y-x\rangle + \frac{L}{2}||x-y||^2$$

则称 是 L Smooth 的。

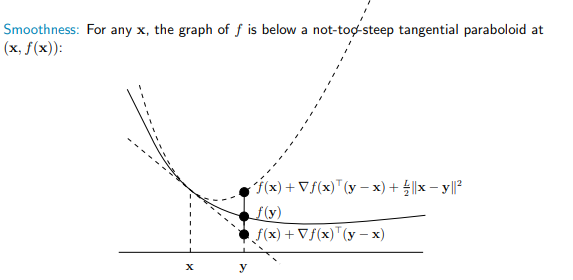
如图所示，Smoothness 是函数在切点处画出的二次曲线，作为函数的上界。 取值越大，则上界越高，越不光滑；而 取值越小，则上界越接近切线，函数越光滑。

事实上，Smoothness 即在函数梯度上的 Lipschitz Continuity，即

$$\langle\nabla f(x)-\nabla f(y),x-y\rangle\leq L||x-y||^2$$

在这里我们给出以上两个关系的等价性证明。

一方面，当梯度满足 Lipschitz Continuity 时，由于 为凸函数，定义域为凸，故令 连线之间某处函数值为

$$h(t) = f(x+t(y-x)),\quad t\in[0,1]$$

利用 Lipschitz Continuity 性质，有

$$\begin{aligned} \nabla h(t)-\nabla h(0) & = \langle \nabla f(x+t(y-x)) - \nabla f(x), y-x \rangle \\ & = \frac{L}{t}\langle \nabla f(x+t(y-x)) - \nabla f(x), t(y-x) \rangle \\ & \leq \frac{L}{t} ||t(y-x)||^2 \\ & = tL||x-y||^2 \end{aligned}$$

因此构造积分

$$\begin{aligned} f(y) & = h(1) \\ & = h(0) + \int_0^1 \nabla h(t) \cdot dt \\ & = h(0) + \int_0^1 \nabla h(t)-\nabla h(0) \cdot dt + \int_0^1 \nabla h(0) \cdot dt \\ & \leq h(0) + \int_0^1 tL||x-y||^2 \cdot dt + \int_0^1 \nabla h(0) \cdot dt \\ & = h(0) + \nabla h(0) + \frac{L}{2}||x-y||^2 \\ & = f(x) + \langle\nabla f(0),y-x\rangle + \frac{L}{2}||x-y||^2 \end{aligned}$$

于是 Smoothness 得证。

另一方面，当函数满足 Smoothness 时，有

$$f(y)\leq f(x)+\langle\nabla f(x),y-x\rangle + \frac{L}{2}||x-y||^2$$

交换 和 ，有

$$f(x)\leq f(y)+\langle\nabla f(y),x-y\rangle + \frac{L}{2}||x-y||^2$$

两式相加即可得到

$$\langle\nabla f(x)-\nabla f(y),x-y\rangle \leq L||x-y||^2$$

于是梯度 Lipschitz Continuity 得证。

综上所述，函数 Smoothness 即为函数梯度 Lipschitz Continuity。

Convergence

考虑上一节中提出的 Smoothness，我们虽然不知道函数 的细节，但是我们可以利用 Smoothness 来最小化误差上界。首先，我们假设 是 Smooth 的，有

$$\left\{ \begin{aligned} &\ f(x_{t+1})\leq f(x_t)+\langle g_t,x_{t+1}-x_t\rangle + \frac{L}{2}||x_{t+1}-x_t||^2 \\ &\ ||x_0-x^*||\leq R \end{aligned} \right.$$

最小化 Smoothness 上界，简写为 RHS，得到

$$\frac{\partial \text{RHS}(x_{t+1})}{\partial x_{t+1}} = g_t + L(x_{t+1}-x_t) = 0$$

即

$$x_{t+1} = x_t - \frac{1}{L}\nabla f(x_t)$$

可以证明，当 是 Smooth 的时候，上述迭代式是收敛的，且收敛速度为 。

以下给出证明：

由于 是 Smooth 的，可以约束 Vanilla Analysis 中 ，有

$$f(x_{t+1}) - f(x_t) \leq \langle g_t, x_{t+1} - x_t \rangle + \frac{L}{2} ||x_{t+1} - x_t||^2$$

代入 ，有

$$f(x_{t+1}) - f(x_t) \leq -\frac{1}{2L} ||g_t||^2$$

即

$$||g_t||^2\leq 2L(f(x_{t}) - f(x_{t+1}))$$

代回 Vanilla Analysis，有

$$\begin{aligned} \sum_{t=0}^{T-1}\left( f(x_t)-f(x^*) \right) & \leq \frac{\gamma}{2} \sum_{t=0}^{T-1}||g_t||^2 + \frac{1}{2\gamma} ||x_0-x^*||^2 \\ & = \frac{1}{2L} \sum_{t=0}^{T-1} ||g_t||^2 + \frac{L}{2} ||x_0-x^*||^2 \\ & \leq \sum_{t=0}^{T-1} \left(f(x_{t})-f(x_{t+1})\right) + \frac{L}{2} ||x_0-x^*||^2 \\ & = f(x_{0})-f(x_{T}) + \frac{L}{2} ||x_0-x^*||^2 \\ \end{aligned}$$

移项得

$$\sum_{t=1}^{T}\left( f(x_t)-f(x^*) \right) \leq \frac{L}{2} ||x_0-x^*||^2 = \frac{LR^2}{2}$$

由于迭代式每一步都是最小化上界，因此最后一步一定是最优的，即

$$f(x_T)-f(x^*) \leq \frac{1}{T}\left(\sum_{t=1}^{T}\left( f(x_t)-f(x^*) \right)\right) \leq \frac{LR^2}{2T}$$

要使得误差降低到 以下，则有

$$f(x_T)-f(x^*) \leq \frac{LR^2}{2T} \leq \epsilon \Rightarrow T\geq \frac{LR^2}{2\epsilon}$$

于是得到收敛率

$$T\sim \mathcal{O}(\frac{1}{\epsilon})$$

Smooth and Strongly Convex Functions

Strongly Convex

对于处处可导的函数 ，如果满足

$$f(y)\geq f(x)+\langle\nabla f(x),y-x\rangle + \frac{\mu}{2}||x-y||^2$$

则称 是 Strongly Convex 的。

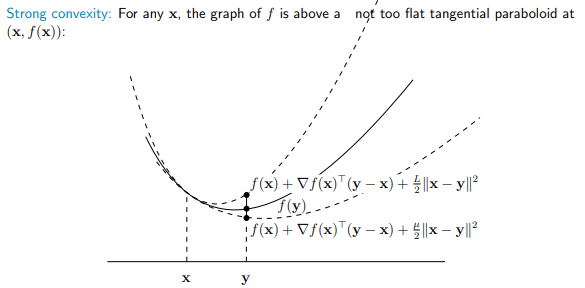
如图所示，Strongly Convex 是一个比 Convex 更强的下界。当一个函数既是 Strongly Convex 又是 Smooth 的时，直觉上这个函数的变化范围应该更小，因此收敛速度应该更快。

Convergence

假设我们的目标函数是 Smooth 且 Strongly Convex 的，则

$$\left\{ \begin{aligned} &\ f(x_{t+1})\leq f(x_t)+\langle g_t,x_{t+1}-x_t\rangle + \frac{L}{2}||x_{t+1}-x_t||^2 \\ &\ f(x_{t+1})\geq f(x_t)+\langle g_t,x_{t+1}-x_t\rangle + \frac{\mu}{2}||x_{t+1}-x_t||^2 \\ &\ ||x_0-x^*||\leq R \end{aligned} \right.$$

使用上一节所得的迭代式，即

$$x_{t+1} = x_t - \frac{1}{L}\nabla f(x_t)$$

可以证明，上述迭代式是收敛的，且收敛速度为 。

以下给出证明：

由 Vanilla Analysis 有

$$\langle g_t,x_t-x^* \rangle = \frac{\gamma}{2} ||g_t||^2 + \frac{1}{2\gamma} \left(||x_t-x^*||^2-||x_{t+1}-x^*||^2 \right)$$

由 Strongly Convex 有

$$\langle g_t,x_{t}-x^* \rangle \geq f(x_t) - f(x^*) + \frac{\mu}{2}||x_{t}-x^*||^2$$

代入 Vanilla Analysis，有

$$f(x_t) - f(x^*) \leq \frac{\gamma}{2} ||g_t||^2 + \frac{1}{2\gamma} \left(||x_t-x^*||^2-||x_{t+1}-x^*||^2 \right) - \frac{\mu}{2}||x_{t}-x^*||^2$$

整理得

$$\underline{||x_{t+1}-x^*||^2} \leq 2\gamma\left(f(x^*) - f(x_t)\right) + \gamma^2||g_t||^2 + \underline{(1-\mu\gamma)||x_t-x^*||^2}$$

考虑噪声项

$$\begin{aligned} 2\gamma\left(f(x^*) - f(x_t)\right) + \gamma^2||g_t||^2 & = \frac{2}{L}\left(f(x^*) - f(x_t)\right) + \frac{1}{L^2}||g_t||^2 \\ & \leq \frac{2}{L}\left(f(x_{t+1}) - f(x_t)\right) + \frac{1}{L^2}||g_t||^2 \\ & \leq - \frac{1}{L^2}||g_t||^2 + \frac{1}{L^2}||g_t||^2 \\ & = 0 \end{aligned}$$

因此有

$$||x_{t+1}-x^*||^2 \leq(1-\mu\gamma)||x_t-x^*||^2 = \left(1-\frac{\mu}{L}\right)||x_t-x^*||^2$$

连乘展开得

$$||x_{T}-x^*||^2 \leq \left(1-\frac{\mu}{L}\right)^2||x_0-x^*||^2$$

由 Smoothness 且 ，有

$$f(x_T)-f(x^*) \leq \langle\nabla f(x^*),x_T-x^* \rangle + \frac{L}{2}||x_T-x^*||^2 = \frac{L}{2}||x_T-x^*||^2$$

代入上式，有

$$f(x_T)-f(x^*) \leq \frac{L}{2}\left(1-\frac{\mu}{L}\right)^2||x_0-x^*||^2 \leq \frac{L}{2}\left(1-\frac{\mu}{L}\right)^2R^2$$

要使得误差降低到 以下，则有

$$f(x_T)-f(x^*) \leq \frac{L}{2}\left(1-\frac{\mu}{L}\right)^2R^2 \leq \epsilon \Rightarrow T\geq \frac{L}{\mu}\ln\left(\frac{LR^2}{2\epsilon}\right)$$

于是得到收敛率

$$T\sim \mathcal{O}(\log\frac{1}{\epsilon})$$