无监督学习-2-聚类与EM算法

聚类

聚类同样是密度估计的一种。不同于前文所述的密度估计算法，聚类将数据分进多个分布中，每个分布即聚类所得的类。

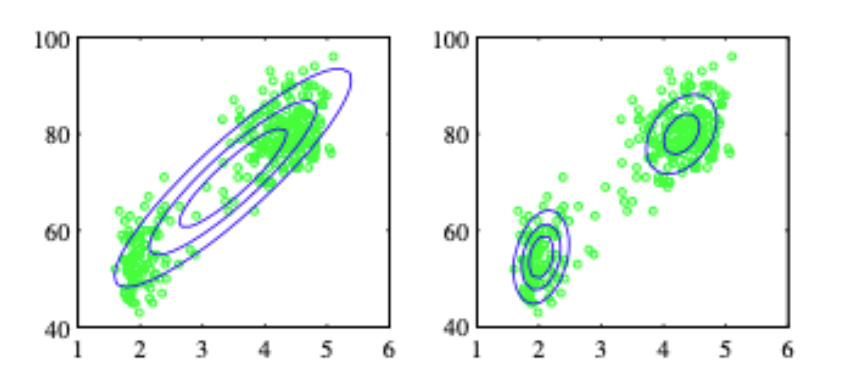
如图所示，上图是著名的 Old Faithful 数据集。真实的数据分布往往难以用一个分布（左）去刻画，因而使用 GMM 等将数据用多个分布（右）进行刻画的算法往往在实际运用中更有意义。

本文中将介绍两种聚类算法：K-means 和 GMM，并给出 ELBO 与 EM 算法的推导，用于求解含隐变量的参数估计问题。

模型

K-means

• 目标：将数据集 分为 类，样本 被分入 类，并使用各类的代表元素 代表类。
• 算法
  • 初始化：随机初始化
  • 循环以下步骤，直到算法收敛
    • E-step: 将每个样本分配给最近的代表元素所在类 $c_i=\arg\min_k ||x_i-\mu_k||^2$
    • M-step: 更新每个类的代表元素为类内元素的均值 $\mu_k=\frac{\sum_i x_i\mathbb{I}(c_i=k)}{\sum_i \mathbb{I}(c_i=k)}$

高斯混合模型 (Guassian Mixture Model, GMM)

• 目标：将数据集 分为 类，每个样本被分入 类的概率为 ，并使用 表示第 类服从高斯分布 。即样本服从高斯分布的线性组合： $$f_X(x_i)=\sum_{k=1}^K\pi_k\mathcal{N}(\mu_k,\sigma^2_k)$$
• 算法
  • 初始化：随机初始化
  • 循环以下步骤，直到算法收敛
    • E-step: 计算隐变量分布 $\gamma_{i,k} = \frac{\pi_k\mathcal{N}(x_i;\mu_k,\sigma_k^2)}{\sum_{j=1}^K\pi_j\mathcal{N}(x_i;\mu_k,\sigma_k^2)}$
    • M-step: 更新每个类的代表元素为类内元素的均值 $$\left\{\begin{aligned} & \pi_j = \frac{1}{n}\sum_{i=1}^n\gamma_{i,j}, &\forall j \\ & \mu_j = \frac{\sum_{i=1}^n\gamma_{i,j}x_i}{\sum_{i=1}^n\gamma_{i,j}}, &\forall j \\ & \sigma_j = \frac{\sum_{i=1}^n\gamma_{i,j}||x_i-\mu_k||^2}{\sum_{i=1}^n\gamma_{i,j}}, &\forall j \end{aligned}\right.$$

EM 算法与 GMM 的解

要求 GMM 的参数，容易想到的方法使用 MLE 求解，即

$$\mathcal{L}(X;\pi,\mu,\sigma) = \sum_{i=1}^n\log\left(\sum_{k=1}^K\pi_k\mathcal{N}(x_i;\mu_k,\sigma_k^2)\right)\quad\texttt{s.t.}\quad \sum_k\pi_k=1$$

但是此目标函数即难以求解闭式解，又因为在求导时容易出现 或者 ，所以难以进行梯度下降。

考虑其他方式进行求解，观察到事实上从混合高斯分布中采样数据时可以分为两步

• 从多项分布中采样得到类别
• 从类别对应的高斯分布中采样得到样本

其中 是我们能观察到的样本，而 则是无法观测的隐变量。此时有 的边际概率分布

$$f_Z(z)=\pi_z=\prod_{k=1}^K\pi_z^{\mathbb{I}(z=k)}$$

以及条件概率分布

$$f_{X|Z}(x|Z=z)= \mathcal{N}(x;\mu_z,\sigma_z^2) =\prod_{k=1}^K\mathcal{N}(x;\mu_z,\sigma_z^2)^{\mathbb{I}(z=k)}$$

则可得联合分布

$$f_{(X,Z)}(x,z)=\prod_{k=1}^K\left(\pi_k\mathcal{N}(x;\mu_z,\sigma_z^2)\right)^{\mathbb{I}(z=k)}$$

如果我们可以观测到完整的样本 ，可用 MLE 求解，即

$$\max_\theta \mathcal{L}(X,Z;\theta) = \sum_{i=1}^n\sum_{j=1}^K\mathbb{I}(z=k)\left(\log\pi_k+\log\mathcal{N}(x;\mu_z,\sigma_z^2)\right)\quad\texttt{s.t.}\quad \sum_k\pi_k=1$$

然而我们并不知道 ，在这种只能观测到样本部分参数的时候可以使用EM算法进行求解。在下一节中，我们会证明使用 EM 算法所得的优化目标等同于没有隐变量 时的优化目标。但在本节中，我们先聚焦于 EM 算法的使用，来推导 GMM 。

E-step

首先计算

$$\begin{split} Q(\theta,\theta^{(t)}) & =\mathbb{E}_{Z|X,\theta^{(t)}}\left[\mathcal{L}(X,Z;\theta)\right] \\ & =\mathbb{E}_{Z|X,\theta^{(t)}}\left[\sum_{i=1}^{n} \sum_{k=1}^{K}\mathbb{I}(Z_i=k)(\log\pi_k+\log\mathcal{N}(x;\mu_k,\sigma_k^2))\right] \\ & =\sum_{i=1}^{n} \sum_{k=1}^{K}\mathbb{E}_{Z|X,\theta^{(t)}}\left[\mathbb{I}(Z_i=k)\right] (\log\pi_k+\log\mathcal{N}(x;\mu_k,\sigma_k^2)) \end{split}$$

其中

$$\begin{split} \mathbb{E}_{Z|X,\theta^{(t)}}\left[\mathbb{I}(Z_i=k)\right] & = \frac{P\left(Z_i=k,X_i\mid\theta^{(t)}\right)}{P\left(X_i\mid\theta^{(t)}\right)} \\ & = \frac{P\left(Z_i=k,X_i\mid\theta^{(t)}\right)}{\sum_{j=1}^KP\left(Z_i=j,X_i\mid\theta^{(t)}\right)} \\ & = \frac{\pi_k\mathcal{N}(x;\mu_k^{(t)},{\sigma_k^{(t)}}^2)}{\sum_{j=1}^K\pi_j\mathcal{N}(x;\mu_j^{(t)},{\sigma_j^{(t)}}^2)}\\ & = \gamma_{i,k}^{(t+1)} \end{split}$$

于是有

$$Q(\theta,\theta^{(t)})=\sum_{i=1}^{n} \sum_{k=1}^{K}\gamma_{i,k}^{(t+1)} (\log\pi_k+\log\mathcal{N}(x;\mu_k,\sigma_k^2))$$

M-step

最大化 函数，使用拉格朗日乘子法求解上述带等式约束最大化问题，有

$$\arg\max_{\xi,\theta}L(\theta, \xi) = Q(\theta,\theta^{(t)}) - \xi\left(\sum_{j=1}^{K}\pi_j-1\right)$$

代入求导求解，可得

$$\left\{\begin{aligned} & \pi_j = \frac{1}{n}\sum_{i=1}^n\gamma_{i,j}, &\forall j \\ & \mu_j = \frac{\sum_{i=1}^n\gamma_{i,j}x_i}{\sum_{i=1}^n\gamma_{i,j}}, &\forall j \\ & \sigma_j = \frac{\sum_{i=1}^n\gamma_{i,j}||x_i-\mu_k||^2}{\sum_{i=1}^n\gamma_{i,j}}, &\forall j \end{aligned}\right.$$

EM算法和ELBO

在上一节中，我们仅仅给出了使用 EM 算法解带隐变量问题的一个实例，但是并没有给出完整的推导。在本节中，我们将从头开始给出完整的推导。

推导

考虑由可观测 和隐变量 组成的数据集 ，如果不考虑隐藏数据，可以直接使用MLE求解

$$\max_\theta \mathcal{L}(X;\theta) = \max_\theta\sum_{i=1}^n\log P(x_i|\theta)$$

但因为隐藏数据存在，有

$$P(X|\theta) = \int_ZP(Z,X|\theta)dZ$$

如果将上式带入优化目标中，在 中会出现求和或积分符号，难以求导从而求解。对于这种无法直接求解的问题，我们通常会采用迭代求解的策略，一步一步逼近最终的结果，在 EM 算法中就是 E 步和 M 步的交替进行，直至收敛。

在 EM 算法中，一个重要的问题就是通过可观测的样本 推断隐变量的分布 ，根据条件概率公式即

$$P(X|\theta) = \frac{P(X,Z|\theta)}{P(Z|X,\theta)}$$

两边同时取对数

$$\log P(X|\theta) = \log P(X,Z|\theta) - \log P(Z|X,\theta)$$

引入 的分布 ( 满足 )，有

$$\log P(X|\theta) = \log \frac{P(X,Z|\theta)}{q(Z)} - \log \frac{P(Z|X,\theta)}{q(Z)}$$

两把同时对 求期望，有

$$\mathbb{E}_Z\left[\log P(X|\theta)\right] = \mathbb{E}_Z\left[\log \frac{P(X,Z|\theta)}{q(Z)}\right] - \mathbb{E}_Z\left[\log \frac{P(Z|X,\theta)}{q(Z)}\right]$$

展开成积分形式，有

$$\int_Z q(Z)\log P(X|\theta) dZ = \int_Z q(Z)\log \frac{P(X,Z|\theta)}{q(Z)} dZ - \int_Z q(Z)\log \frac{P(Z|X,\theta)}{q(Z)} dZ$$

观察到最左边项 和 无关可以直接去掉积分；最右边项实际上是关于 和 的 。于是原式可以改写为

$$\log P(X|\theta)= \int_Z q(Z)\log \frac{P(X,Z|\theta)}{q(Z)} dZ - D_{KL}\left(q(Z)||P(Z|X,\theta)\right)$$

由于 KL 散度非负，因此得到了 的一个下界，即 (ELBO)

$$\log P(X|\theta)\geq \int_Z q(Z)\log \frac{P(X,Z|\theta)}{q(Z)} dZ$$

通过迭代提高 ELBO 项，即可使得 增大。然而这里我们仍然不知道 的分布，无法直接最大化 ELBO。如果令 ，则 KL 散度项为 0，可将下界抬高到优化目标处，此时再最大化 ELBO，可以最大化在 上的增益。在迭代过程中，我们有上一轮迭代所得的 ，于是令 可以得到 ELBO 如下

$$\texttt{ELBO} = \int_Z P(Z|X,\theta^{(t)})\log \frac{P(X,Z|\theta)}{P(Z|X,\theta^{(t)})} dZ = \mathbb{E}_{Z|X,\theta^{(t)}}\left[\log \frac{P(X,Z|\theta)}{P(Z|X,\theta^{(t)})}\right]$$

展开得到

$$\texttt{ELBO} = \mathbb{E}_{Z|X,\theta^{(t)}}\left[\log P(X,Z|\theta)\right] + \mathbb{E}_{Z|X,\theta^{(t)}}\left[\log P(Z|X,\theta^{(t)})\right]$$

其中第二项与优化目标无关，忽略，因此得到

$$\texttt{ELBO} = \mathbb{E}_{Z|X,\theta^{(t)}}\left[\log P(Z|X,\theta^{(t)})\right]$$

由此我们可以得到 EM 算法的两个步骤：

• E-step 时令 ，抬高 ELBO 至优化目标 ，计算

  $$Q(\theta,\theta^{(t)}) = \mathbb{E}_{Z|X,\theta^{(t)}}\left[\log P(Z|X,\theta^{(t)})\right]$$

• M-step 时迭代计算新的参数值

  $$\theta^{(t+1)} = \arg\max_\theta Q(\theta,\theta^{(t)})$$

至此，我们理解了 EM 算法中 E 步和 M 步的具体数学含义。

• 从过程上说，我们实质上通过 E-M 的交替迭代来规避了 MLE 过程中隐变量的积分或求和：在 E 步通过固定待求参数 来估计隐变量分布；在 M 步通过固定隐变量分布来使用 MLE 求解参数。
• 从形式上说，我们将 拆分成为联合分布 与 KL 散度，计算 ELBO （也就是联合分布）的条件概率期望作为难以求导的原优化问题的替代，降低了计算难度。

收敛性

要证明 EM 算法的收敛性，首先要证明我们的对数似然函数在迭代过程中单调增，即

$$\mathcal{L}(X|\theta^{(t+1)}) \geq \mathcal{L}(X|\theta^{(t)})$$

以下给出证明，考虑

$$P(X|\theta) = \frac{P(X,Z|\theta)}{P(Z|X,\theta)}$$

同时取 ，并对 求期望整理后得

$$\mathcal{L}(X|\theta) = Q(\theta,\theta^{(t)}) - H(\theta,\theta^{(t)})$$

其中

$$H(\theta,\theta^{(t)}) = \mathbb{E}_{Z|X,\theta^{(t)}}\left[\mathcal{L}(Z|X,\theta)\right]$$

所以有

$$\mathcal{L}(X|\theta^{(t+1)}) - \mathcal{L}(X|\theta^{(t)}) = \left(Q(\theta^{(t+1)},\theta^{(t)}) - Q(\theta^{(t)},\theta^{(t)})\right) - \left(H(\theta^{(t+1)},\theta^{(t)}) - H(\theta^{(t)},\theta^{(t)})\right)$$

由 定义可知

$$Q(\theta^{(t+1)},\theta^{(t)}) - Q(\theta^{(t)},\theta^{(t)}) \geq 0$$

且

$$\begin{split} H(\theta^{(t+1)},\theta^{(t)}) - H(\theta^{(t)},\theta^{(t)}) & = \mathbb{E}_{Z|X,\theta^{(t)}}\left[\mathcal{L}(Z|X,\theta^{(t+1)})-\mathcal{L}(Z|X,\theta^{(t)})\right] \\ & = \mathbb{E}_{Z|X,\theta^{(t)}}\left[ \log \left(\frac{P(Z|X,\theta^{(t+1)})}{P(Z|X,\theta^{(t)})}\right) \right] \\ & \mathop{\leq}\limits_{(Jenson)} \log\left(\mathbb{E}_{Z|X,\theta^{(t)}}\left[ \frac{P(Z|X,\theta^{(t+1)})}{P(Z|X,\theta^{(t)})} \right]\right) \\ & = \log\left(\int_Z P(Z|X,\theta^{(t)})\frac{P(Z|X,\theta^{(t+1)})}{P(Z|X,\theta^{(t)})} dZ\right) \\ & = \log\left(\int_Z P(Z|X,\theta^{(t+1)}) dZ\right) \\ & = \log 1 \\ & = 0 \end{split}$$

从而

$$\mathcal{L}(X|\theta^{(t+1)}) \geq \mathcal{L}(X|\theta^{(t)})$$

得证。

但需要说明的是，这里的单调性并不能保证算法收敛到全局最优解，因此在实际使用过程中，需要一个较好的初始化才能收敛到一个较好的解。