强化学习DQN系列小结

前言

DQN 作为 value-based 的强化学习方法，擅长处理离散情境下的强化学习问题。其本质是 deep learning 版本的 Q-learning，所以其基本模型和 Q-learning 类似，基于TD时间差分设置目标函数，并 的贪心策略进行探索和学习。在此基础上利用深度学习的优势，将难以维护的Q值表用一个神经网络来维护，形成了 Deep Q-Learning（NIPS 2013）。事实上，我们可以认为 deep learning 在其中的主要作用只是替换了 Q 值表，而算法的核心思想仍然可以认为是一种启发式搜索。

在此基础上，Nature DQN (NIPS 2015) 通过解耦目标Q值动作的选择和目标Q值的计算，提高了算法效率。此后又在 Nature DQN 的基础上产生了三种独立的优化策略: Deep Reinforcement Learning with Double Q-learning (AAAI 2016) 在计算 TD 值中的目标 Q值时，先从当前网络中获取动作，再从目标网络中计算；Dueling Network Architectures for Deep Reinforcement Learning (ICML 2016) 将 Q 值拆分成状态值 V 和动作的优势值 A；Prioritized Experience Replay (ICLR 2016) 认为 TD 值越大的样本对训练越有利，所以在经验池中，有更大概率选取那些 TD 值更大的样本进行训练；以上三种方法都优化了原始 DQN ，并且这几种方法可以被组合起来使用，后续的一些工作主要就做了融合的尝试，但是因为这种融合怪工作本身没有其他的创新点，所以这里暂且忽略不表。

基本模型

DQN

DQN 是深度版本的 Q-learning，主要基于 TD 时间差分方法，如果不熟悉时间差分，可以移步本人对强化学习数学模型的介绍 Breif Introduction for Reinforcement Learning (Background Info) 中 Temporal-Difference 一节。

数学记号

为了方便介绍，这里先重新给出接下来要用到的数学记号：

• :状态集合
• : 某状态
• : 动作集合
• : 某动作
• : 状态的回报值
• : 状态采取动作 产生的 值
• : 某策略

公式推导

根据 TD 时间差分方法，我们要最小化当前状态值和目标状态值之间的差，假设当前状态为 ，选取动作为 ，次状态 ， 那么我们容易得到当前值 $y_i'=Q(s_t, a_t)$ 和目标值 $y_i=R(s_{t+1})+Q(s_{t+1},\pi(s_{t+1}))$ 其中 $\pi(s)=\arg\max_a Q(s,a)$ 由此我们得到优化目标 td_error $loss=MSE(y_i,y_i')$ 用该损失函数对 进行梯度下降即可。

算法流程

• S1：初始化 的网络参数，清空经验集合 ，初始化 为初始状态
• S2：计算 ， 根据 得到动作
• S3：根据 得到次状态 ，回报值 ，终止标记 (表示是否走到了终止状态)
• S4：将经验 存入经验集合
• S5：更新状态
• S6：从经验集合中获取一组样本，计算 td_error ，对于走到终止节点的样本，目标 值只需要计算 。即对于样本 ，若 ， $y=r$，反之若 ，$y=r+Q(s',\arg\max_aQ(s',a))$
• S7：根据 td_error 优化 网络参数
• S8：若走到终止状态，根据迭代轮数决定结束训练或初始化 并返回 S2，否则直接返回 S2

Nature DQN

优化思想

在上一节中，DQN 希望用目标 值来训练当前 值，且希望用当前 值来近似目标 值，这样互相依赖的关系不利于训练的进行，因此 Nature DQN 在 DQN 的基础上，将 函数一式两份存储，分别记为 eval_Q ( 以下记作 ) 和 target_Q ( 以下记作 )，分别计算当前值和目标值。开始时先将他们初始化为一样的参数，然后只训练 ，并且定期将 的参数更新到 上。这样就解耦了目标 值和当前 值，使模型有了更强的学习能力。

在实现上，在 DQN 的基础上修改了 S6 中下式 $y=r+Q'(s',\arg\max_aQ'(s,a))$，并在 S7 中更新 。

算法流程

• S1：初始化 的网络参数，复制一份得到 ( 不含梯度信息 )，清空经验集合 ，初始化 为初始状态
• S2：计算 ， 根据 得到动作
• S3：根据 得到次状态 ，回报值 ，终止标记 (表示是否走到了终止状态)
• S4：将经验 存入经验集合
• S5：更新状态
• S6：从经验集合中获取一组样本，计算 td_error ，对于走到终止节点的样本，目标 值只需要计算 。即对于样本 ，若 ， $y=r$，反之若 ，$y=r+Q'(s',\arg\max_aQ'(s',a))$
• S7：根据 td_error 优化 网络参数，根据迭代轮数决定是否用 覆盖 的参数
• S8：若走到终止状态，根据迭代轮数决定结束训练或初始化 并返回 S2，否则直接返回 S2

  三大优化

  Double DQN

  优化思想

  之前的 DQN 存在这样一个问题：目标 值的计算是否准确？全部通过 来计算有没有问题？Double DQN 证明了之前的算法中，直接使用 来计算，容易出现过拟合的情形，所以 DDQN 的作者对 Nature DQN 又进行了一点改动：先用 来选择动作，再用 来计算目标值，通过解耦目标 值动作的选择和目标 值的计算，来达到消除过度估计的问题。

在实现上，在 Nature DQN 的基础上修改了 S6 中下式 $y=r+Q'(s',\arg\max_aQ(s',a))$

算法流程

• S1：初始化 的网络参数，复制一份得到 ( 不含梯度信息 )，清空经验集合 ，初始化 为初始状态
• S2：计算 ， 根据 得到动作
• S3：根据 得到次状态 ，回报值 ，终止标记 (表示是否走到了终止状态)
• S4：将经验 存入经验集合
• S5：更新状态
• S6：从经验集合中获取一组样本，计算 td_error ，对于走到终止节点的样本，目标 值只需要计算 。即对于样本 ，若 ， $y=r$，反之若 ，$y=r+Q'(s',\arg\max_aQ(s',a))$
• S7：根据 td_error 优化 网络参数，根据迭代轮数决定是否用 覆盖 的参数
• S8：若走到终止状态，根据迭代轮数决定结束训练或初始化 并返回 S2，否则直接返回 S2

Dueling DQN

优化思想

我们用 值同时代表状态和动作的价值，那么状态和动作的评估如果分别进行评估会不会更准确？因此 Dueling DQN 提出将 分解为

$$Q(s,a,\theta)=V(s,\theta,\alpha)+A(s,a,\theta,\beta)$$

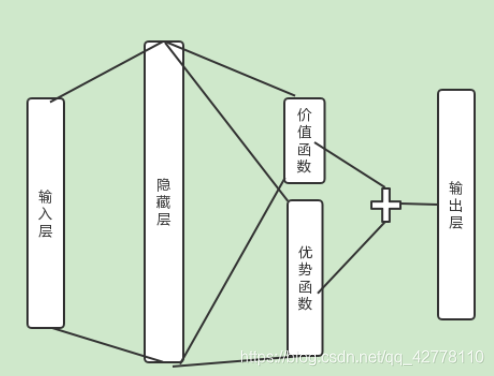
其中 是网络公共参数， 和 是状态值函数 和动作优势函数 各自的网络参数。在实际计算时，一般将动作优势函数的期望归零，即减去状态 下动作优势向量 的均值 $Q(s,a)=V(s)+A(s,a)-mean(A(s))$

其他实现均与 Nature DQN 一致，所以省略算法流程部分。

Prioritized Replay DQN

优化思想

另一个问题时，训练时随机采样的方法好吗？按道理不同样本的重要性是不一样的。Prioritized Replay DQN 提出学习的样本 TD 误差越大，学习效果越好。因此可以用一棵二叉树来维护所有样本，叶子节点上记录样本，其他节点记录重要性，即该子树下样本的 TD 误差之和。训练时，按照节点值大小按概率选取。

需要说明的是，随着模型更新，TD 误差也会发生变化，所以需要定期进行更新。

其他实现均与 Nature DQN 一致，所以省略算法流程部分。

总结

DQN 一系的算法大致沿着 DQN -> Nature DQN -> Double DQN 的顺序进行，他们的主要区别在于 TD 误差的计算式不同，分别为原版的

$$|Q(s,a)-r-Q(s',\arg\max_aQ(s,a))|$$

Nature DQN 对目标 和当前 解耦后的

$$|Q(s,a)-r-Q'(s',\arg\max_aQ'(s,a))|$$

以及 Double DQN 对目标 值动作的选择和目标 值的计算解耦后的

$$|Q(s,a)-r-Q'(s',\arg\max_aQ(s,a))|$$

修改在算法上很微小，只影响了几个 头上的撇，但是其思路却大有门道，值得学习。

此外，Dueling DQN 和 Prioritized Replay DQN 分别优化了 值本身的计算式和学习样本的选取策略，独立地提升了模型的学习能力。在此之外还有其他的优化技巧，但不如介绍的几种流行。

DQN 比较好地代表了基于值（value-based）的深度强化学习流派，但是这类方法

• 擅长处理离散动作，难以处理连续动作空间
• 需要人工设计状态，这样的状态未必合适
• 只能解决确定策略，无法解决随机策略问题

这时我们只能通过其他方法进行学习，比较常见的解决方案是 policy-based methods。

参考文献

本文在书写过程中参考了相关论文，ICML2016 Tutorial: Deep Reinforcement Learning和Pinard的博客。